SELU vs RELU activation in simple NLP models

Background on SELU

Normalized outputs seem to be really helpful in stabilizing the training process. That’s the main reason behind the popularity of BatchNormalization. SELU is a way to output the normalized activations to the next layer.

The overall function is really simple:

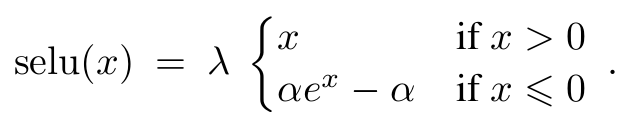
For mean 0 and stdev 1 inputs, the values of α and λ come out to be 1.6732632423543772848170429916717 and 1.0507009873554804934193349852946 respectively.

# PyTorch implementation
import torch.nn.functional as F

def selu(x):
    alpha = 1.6732632423543772848170429916717
    scale = 1.0507009873554804934193349852946
    return scale * F.elu(x, alpha)

# Numpy implementation
import numpy as np

def selu(x):
    alpha = 1.6732632423543772848170429916717
    scale = 1.0507009873554804934193349852946
    return scale * ((x > 0)*x + (x <= 0) * (alpha * np.exp(x) - alpha))

SNLI dataset

SNLI dataset is a collection of 570k english sentence pairs. The task is to classify each pair as either:

• entailment - “A soccer game with multiple males playing.” and “Some men are playing a sport.”
• contradiction - “A man inspects the uniform of a figure in some East Asian country.” and “The man is sleeping.”
• neutral - “A smiling costumed woman is holding an umbrella.” and “A happy woman in a fairy costume holds an umbrella.”

Model Architecture

I am using a simple Bag of words model written in keras. The following python snippet describes the major components. This code is taken from Stephen Merity’s repo here.

# Embedding layer
embed = Embedding(VOCAB, EMBED_HIDDEN_SIZE, weights=[embedding_matrix], input_length=MAX_LEN, trainable=False)
# A dense layer applied over each sequence point
translate = TimeDistributed(Dense(SENT_HIDDEN_SIZE, activation=ACTIVATION))
# A layer to sum up the sequence of words
rnn = keras.layers.core.Lambda(lambda x: K.sum(x, axis=1), output_shape=(SENT_HIDDEN_SIZE, ))

# 2 pairs of input sentences
premise = Input(shape=(MAX_LEN, ), dtype='int32')
hypothesis = Input(shape=(MAX_LEN, ), dtype='int32')
# Get the word embeddings for each of these 2 pairs
prem = embed(premise)
hypo = embed(hypothesis)
# Apply the Dense layer
prem = translate(prem)
hypo = translate(hypo)
# Sum up the sequence
prem = rnn(prem)
hypo = rnn(hypo)
prem = BatchNormalization()(prem)
hypo = BatchNormalization()(hypo)
# Combined the 2 sentences
joint = concatenate([prem, hypo])
joint = Dropout(DP)(joint)
# Add Few dense layers in the end
for i in range(3):
    joint = Dense(2 * SENT_HIDDEN_SIZE, activation=ACTIVATION, kernel_regularizer=l2(L2)(joint)
    joint = Dropout(DP)(joint)
    joint = BatchNormalization()(joint)

SELU vs RELU results

Code for this excercise is available in this repo.

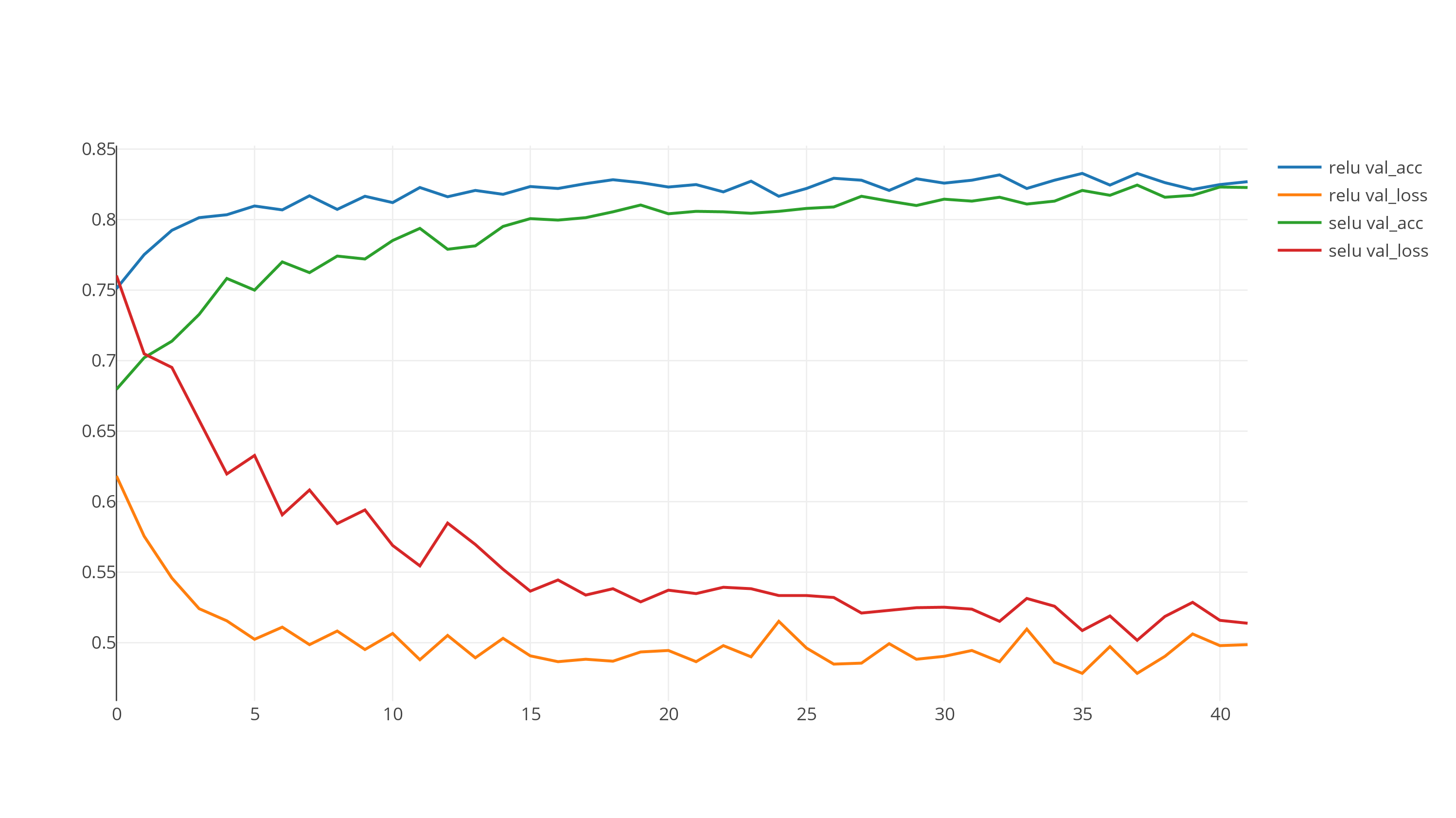
RELU is clearly converging much faster than SELU. My first was to remove the BatchNormalization and do the same comparison. The following graph shows the comparison after removing the BatchNorm components.

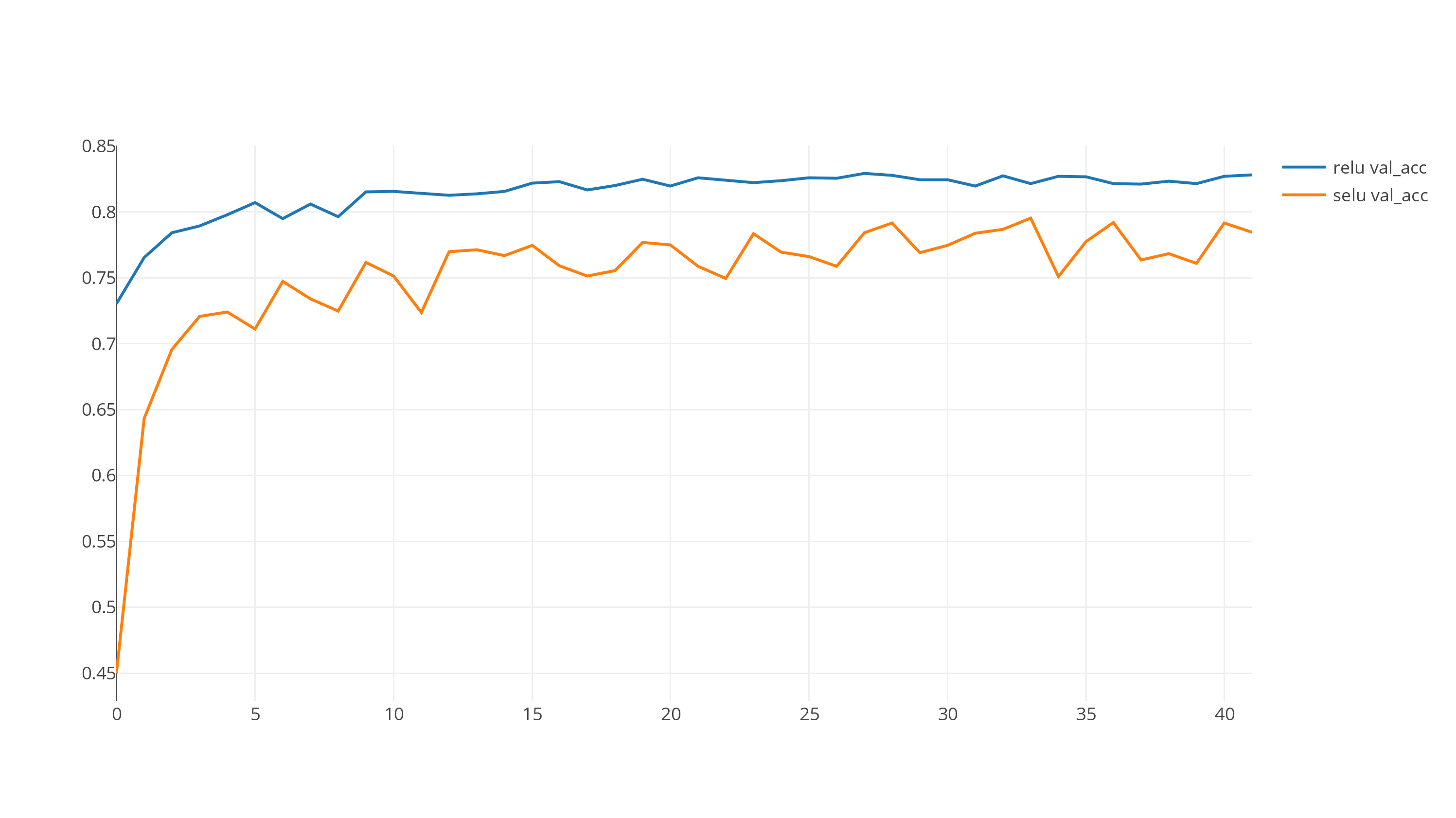
Still, RELU seems to be doing a much better job than SELU for the default configuration.

This behavior remains more or less the same after iterating through hyperparameters. The following graph is for one of the hyperparameter configurations.

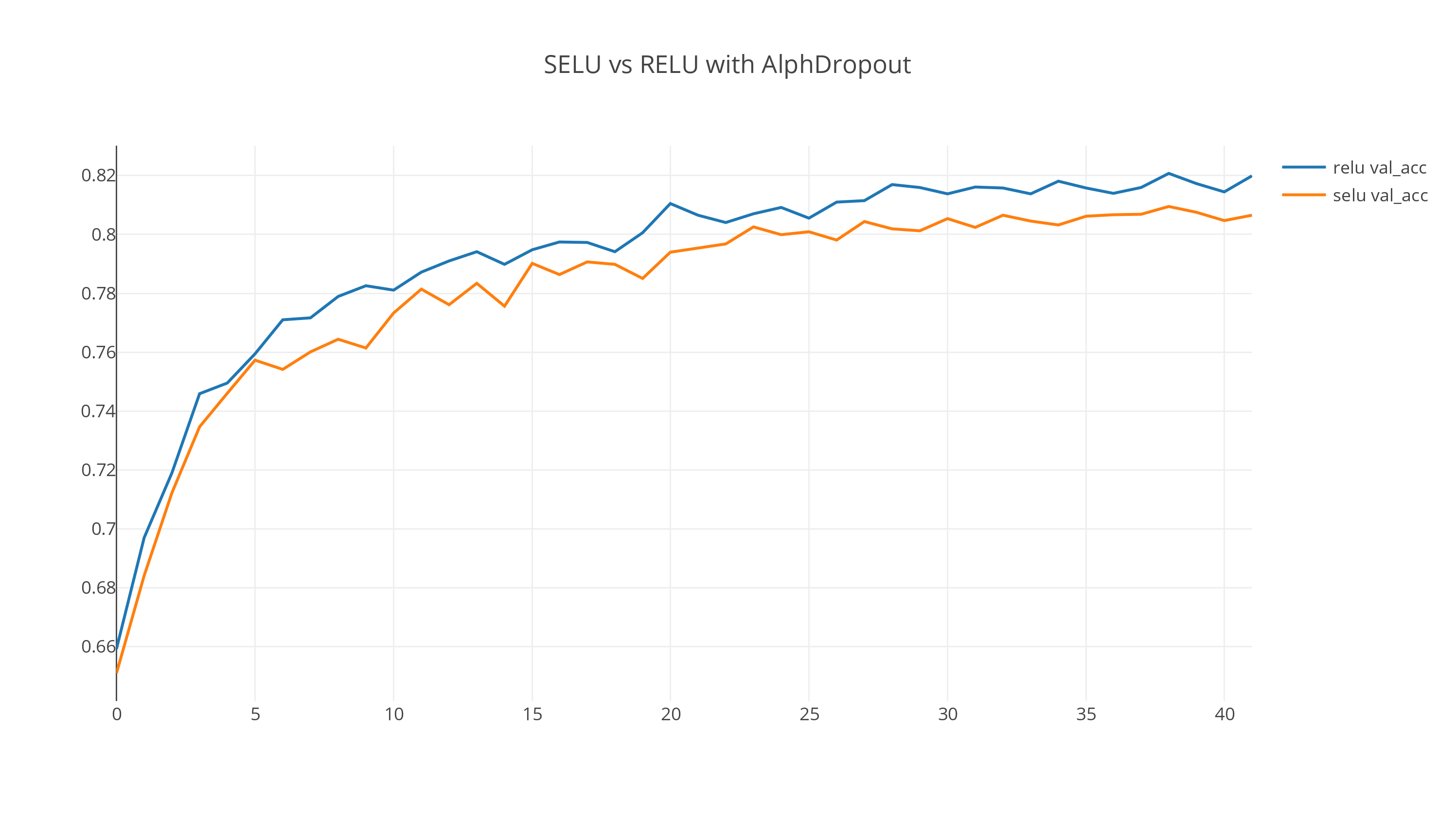
(Edit: I incorporated the suggestion from Dan Ofer below and included the graph with AlphaDropout.)

To be fair, it is still possible that SELU is better in some configurations. Some of the possible reasons are listed below. However, it is clear to me that simply replacing RELU with SELU isn’t going to improve your existing models.

• SELU authors recommend a specific initialization scheme for it to be effective.

Additionally, SELU is a bit more computationally expensive than RELU. On a g2.2xlarge EC2 instance, RELU model took about 49 seconds to complete an epoch, while SELU model took 65 seconds to do the same (33% more).