Hardik Patel

Probability Primer

Discrete Random Variables (RV) and Probability Mass Function (PMF)

Probability Mass Function(PMF) \(P\) maps a state of a random variable to the probability of that random variable taking on that state.

  • Domain of \(P\) is the set of all possible events: \(\Omega\)
  • Probabilities range from 0 to 1. \(\forall{x}\in\mathbf{x}, 0 \le P(x) \le 1\)
  • Probabilities sum up to 1. \(\sum_{x \in \mathbf{x}}P(x) = 1\)

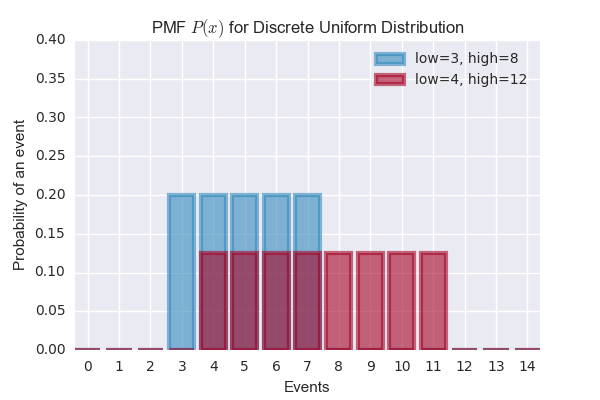
Discrete Uniform Distribution

\[P(\mathbf{x}=x_i) = \frac{1}{k}\] 
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import seaborn as sns
sns.set()

# Discrete Uniform distributions
uniform1 = stats.randint(low=3, high=8)
uniform2 = stats.randint(low=4, high=12)

# Plot the PMF function
a = np.arange(15)
plt.xticks(a + 0.4, a)
plt.bar(a, uniform1.pmf(a), color='#348ABD', edgecolor='#348ABD', alpha=0.60, lw='3', label='low=3, high=8')
plt.bar(a, uniform2.pmf(a), color='#A60628', edgecolor='#A60628', alpha=0.60, lw='3', label='low=4, high=12')
plt.ylim(0, 0.4)
plt.xlabel('Events')
plt.ylabel('Probability of an event')
plt.title('PMF $P(x)$ for Discrete Uniform Distribution')
plt.legend()

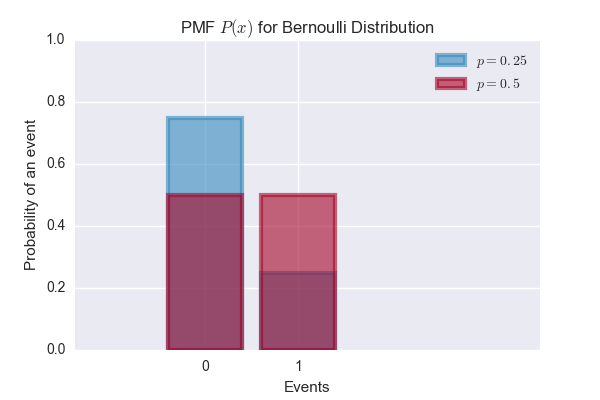
Bernoulli Distribution

\[P(x) = \begin{cases} 1-p, & \text{if $k=0$} \\ p, & \text{if $k=1$} \end{cases}\]

\(p\) is the parameter of the distribution. Expected value of the distribution is \(p\).

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import seaborn as sns
sns.set()

# Bernoulli distributions
bernoulli1 = stats.bernoulli(p=0.25)
bernoulli2 = stats.bernoulli(p=0.5)

# Plot the PMF function
a = np.arange(2)
plt.xticks(a + 0.4, a)
plt.bar(a, bernoulli1.pmf(a), color='#348ABD', edgecolor='#348ABD', alpha=0.60, lw='3', label='$p=0.25$')
plt.bar(a, bernoulli2.pmf(a), color='#A60628', edgecolor='#A60628', alpha=0.60, lw='3', label='$p=0.5$')
plt.xlim(-1, 4)
plt.ylim(0, 1)
plt.xlabel('Events')
plt.ylabel('Probability of an event')
plt.title('PMF $P(x)$ for Bernoulli Distribution')
plt.legend()

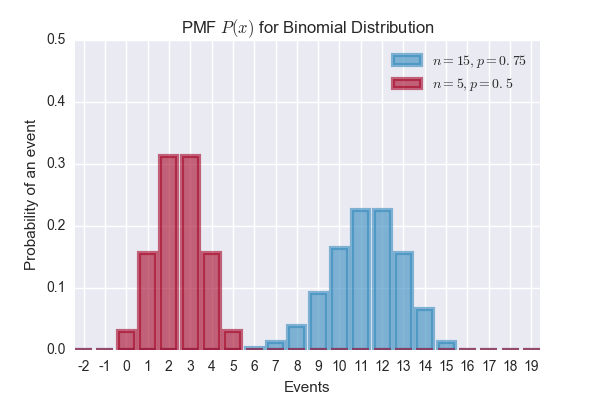
Binomial Distribution

A binomial distribution is parameterized by \(n\) and \(p\). It models the number of successes in a sequence of \(n\) independent experiments, each with success probability \(p\). For \(n=1\), the binomial distribution is a Bernoulli distribution.

\[P(\mathbf{x} = k) = {n \choose k}p^kq^{n-k}, \text{where } k \in \{0, 1, 2,..n\}\] 
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import seaborn as sns
sns.set()

# Binomial distributions
binomial1 = stats.binom(15, 0.75)
binomial2 = stats.binom(5, 0.5)

# Plot the PMF function
a = np.arange(-2, 20)
plt.xticks(a + 0.4, a)
plt.bar(a, binomial1.pmf(a), color='#348ABD', edgecolor='#348ABD', alpha=0.60, lw='3', label='$n=15, p=0.75$')
plt.bar(a, binomial2.pmf(a), color='#A60628', edgecolor='#A60628', alpha=0.60, lw='3', label='$n=5, p=0.5$')
plt.ylim(0, 0.5)
plt.xlabel('Events')
plt.ylabel('Probability of an event')
plt.title('PMF $P(x)$ for Binomial Distribution')
plt.legend()

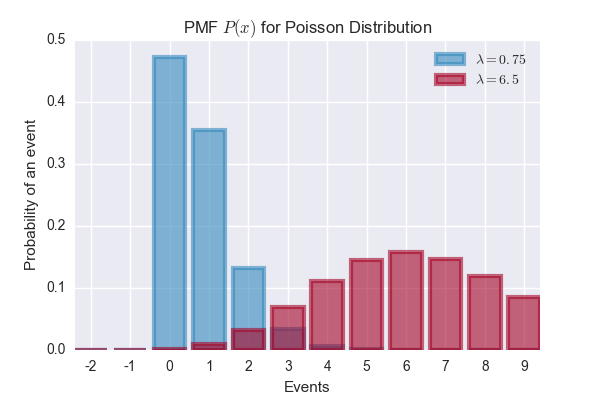
Poisson Distribution

Random Variable \(\mathbf{z}\) is Poisson-distributed if:

\[P(\mathbf{z}=k) = \frac{\lambda^k e^{-\lambda}}{k!}, k = 0, 1, 2,...\]

\(\lambda\) is the parameter of the distribution - it can be any positive number. Expected value of the distribution \(\mathbf{z}\) is:

\[E[\mathbf{z}] = \lambda\] 
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
import seaborn as sns
sns.set()

# Poisson distributions
poisson1 = stats.poisson(0.75)
poisson2 = stats.poisson(6.5)

# Plot the PMF function
a = np.arange(-2, 10)
plt.xticks(a + 0.4, a)
plt.bar(a, poisson1.pmf(a), color='#348ABD', edgecolor='#348ABD', alpha=0.60, lw='3', label='$\lambda=0.75$')
plt.bar(a, poisson2.pmf(a), color='#A60628', edgecolor='#A60628', alpha=0.60, lw='3', label='$\lambda=6.5$')
plt.ylim(0, 0.5)
plt.xlabel('Events')
plt.ylabel('Probability of an event')
plt.title('PMF $P(x)$ for Poisson Distribution')
plt.legend()

Continuous Random Variables and Probability Density Functions (PDF)

We describe continuous random variables using Probabiliy Density Function(PDF) \(p\) instead of probability mass function.

  • It’s important to note that \(p(x)\) is not probability. \(p(x)\) is the probability density.
  • Densities are positive. \(\forall{x}\in\mathbf{x}, p(x) \ge 0\)
  • \(p(x)\delta{x}\) represents the probability of landing inside \(\delta{x}\) sized region. Since \(p(x)\delta{x}\) is the probability, it should integrate to 1. \(\int p(x)dx = 1\)
  • Example: If a random variable \(\mathbf{x}\) is represented by the uniform distribution that takes values from real value \(a\) to real value \(b\), it can be represented as \(\mathbf{x} \sim U(a, b)\).

Uniform Distribution

\[p(x) = \frac{1}{b - a}\]

Exponential Distribution

\[p(x) = e^{-x}, \text{where } x >= 0\]

Normal Distribution

\[p(x) = \frac{e^{-x^2/2}}{\sqrt{2\pi}}\]

Other probability concepts

Marginal Probability

Sometimes we know the probability distribution over a set of variables and we want to know the probability distribution over just a subset of them. The probability distribution over the subset is known as the marginal probability distribution.

\[p(x) = \int p(x, y)dy\]

Considitional Probability

In many cases, we are interested in the probability of some event, given that some other event has happened. This is called a conditional probability.

\[P(\mathbf{y} = y | \mathbf{x} = x) = \frac{P(\mathbf{y} = y, \mathbf{x} = x)}{P(\mathbf{x} = x)}\]

Chain Rule of Probabilities

\[P(a,b,c) = P(a|b,c)P(b|c)P(c)\]

Independence and Conditional Independence

Two random variables \(\mathbf{x}\) and \(\mathbf{y}\) are independent if their probability distribution can be expressed as a product of two factors.

\[\forall x\in\textbf{x},y\in\textbf{y}, p(\textbf{x}=x, \textbf{y}=y) = p(\textbf{x}=x)p(\textbf{y}=y)\]

Expectation, Variance and Covariance

Expected value of a function \(f(x)\) over the random variable \(\textbf{x}\) is defined as:

\[E_{x \sim p}[f(x)] = \int p(x)f(x)dx\]

Bayes’ Rule

\[P(x|y) = \frac{P(x)P(y|x)}{P(y)}\]

Resources